協力する種 その15

協力する種:制度と心の共進化 (叢書《制度を考える》)

第4章　ヒトの協力の社会生物学　その3

矮小化された「血縁に基づく淘汰」では人間の利他性の進化を説明できないが，マルチレベル淘汰では説明できると主張する著者たちは続いてこのマルチレベル淘汰のフレームを記述する．

4.2　マルチレベル淘汰をモデル化する

著者たちは簡単な小グループに分かれた集団において，小グループ内でA（利他）タイプ個体はコストcを払って同グループ内の自分以外のランダムな個体にbを与える．という相互作用を行い．Nタイプ個体は単に受け取るだけという状況を想定する．

ここでAタイプの頻度をp，適応度をw，グループの添え字をj，その中の個体の添え字をiと置く．
そしてベースラインの適応度をβ₀，w_ijに与えるグループのp_iの効果をβ_g，自分のタイプp_ijの効果をβ_i，そしてβ_G=β_g+β_iと置く．

すると相互作用の性質からβ_i=-c，β_g=b，β_G=b-cとなる．

ここで著者たちはプライス方程式から得られたマルチレベル淘汰の基本方程式を示す．

なおこの式についての大槻のコラム「プライス方程式とは」*1がここに挿入されており，どのようにこの式を読むのかが解説されていてわかりやすい．この式になれていない人には必読だ．

これを定常的な個体群の場合にはw=1になること，相互作用の性質からβ_i=-c，β_g=b，β_G=b-cになることから利他的遺伝子の頻度変化△pは以下のように書けることになる．ここでvar(p_ij)に上線がついているのはグループ内分散のグループの大きさにかかる重み付けがあることを示している．

この第1項がグループ間による効果，第2項がグループ内による効果ということになる．

するとこの式を使ってこの相互作用遺伝子が頻度を増すかどうかを知るには，b, c, var(p_i)（グループ間分散）, 上線つきvar(p_ij)（グループ内分散）を知る必要がある．ここで著者たちは後者2つと関連する「分散比」F_ST（利他的個体頻度のグループ間分散の集団全分散に対する比）を導入する．今後の条件判定はこのF_STを用いてなされることになる．集団全分散はグループ間分散とグループ内分散の和になるので

これは集団規模で見た相互作用相手に関する非ランダム度を表すと解釈できる．そしてこの分散比F_STを用いると先ほどの遺伝子頻度変化△pを表す式を用いて，△p>0を変形して利他的遺伝子頻度が増加する条件は次のように書けることになる．これは通常のハミルトン則における血縁度のような役割を果たす．

ここまでのところの記述はこの数理的な結論を著者たちが導き出したかのようである．しかし実はハミルトンの1975年の論文においてほぼ同じ結論が既に明確に述べられている（本書の方がFの定義がより明確に書かれているほか，若干の前提，議論の進め方に違いがあり，著者たちの式の数理的結果の方がより一般化した形になっている．しかしエッセンスは同じだ）ハミルトンはFをグループ内で同じタイプの個体が相互作用する相関として定義した上で，利他的な行動が進化する条件を以下の通りに示している．ここで，ハミルトンが，K, k と置いているパラメータはほぼ b, c と同じであり，実質的にこのボウルズとギンタスの条件式と同じだ．ハミルトンのオリジナルについてはhttp://d.hatena.ne.jp/shorebird/20170625参照

ボウルズとギンタスはこの分散比F_STについて，グループ内での相互作用期待確率で表現すると以下のようになる説明している．（ここでP(A|A)は自分が利他個体であるときに利他個体と相互作用する確率，P(A|N)は自分が利己個体であるときに利他個体と相互作用する確率を表す）これはかなりはしょった説明であり，大槻がコラムで丁寧にその導出を解説している．
これはこの分散比が高いと利他個体同士，利己個体同士がより同じグループに固まる傾向があることを意味することを示している．利他行動の進化の基本条件である「正の同類性」の集団内に相互作用を行うグループ分けがある場合の指標ということになる．
そして今後初期人類においてこの条件が満たされているかどうかについてF_ST，b，c の推定値を当てはめていくことになる．

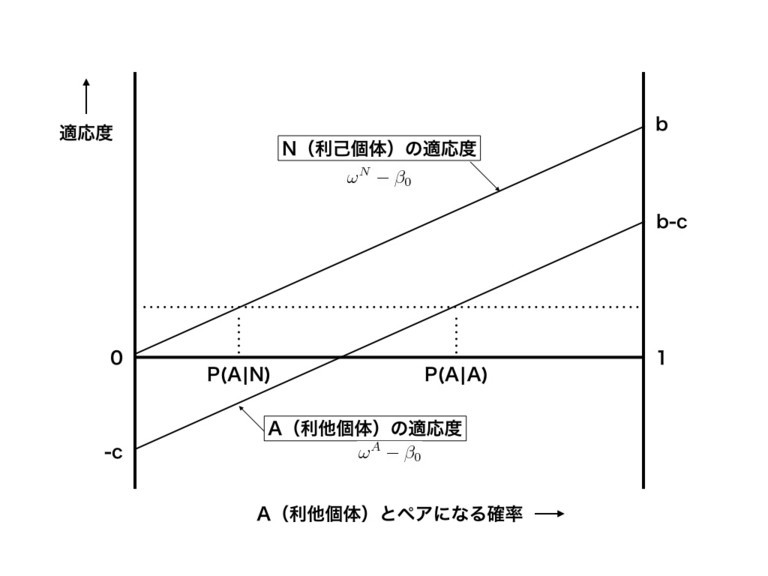
さらに著者たちはこれを直感的に理解できるように図示している．

利他個体とペアになる確率が同じなら，利己個体の方がコストcを払う必要がないので，必ず適応度が高くなる．これをカバーして利他行動遺伝子の頻度が上がるためには b, c に応じたP(A|A)-P(A|N)の幅が必要になるという風に解釈できる．
またこの節の最後では，この条件式は利他行動の進化条件を示すに過ぎず，どのようにどの遺伝子の頻度が増えるのかを記述する力学系にはなっていないことが説明されている．このような進化過程を見るには基本的にはシミュレーションの方式を採ることになるのだ．

この節の記述は数理的なものでマルチレベル淘汰にかかる基本方程式，進化条件式がきちんと記述されていると評価できる．しかしなぜ著者たちは，ほぼ40年も前に基本的に同じ洞察にたどりついていたハミルトンの業績をきちんと紹介しないのだろうか．基本的に本書の記述はハミルトンの1975年のアイデアを（一部の議論を精密化・一般化した上で）焼き直したものものに過ぎない．オリジナルなアイデアに対するリスペクトを欠いたこの姿勢には全くイライラさせられる限りだ．（なお文献リストにはこの1975年のハミルトンの論文も載せられている．あるいは彼等はこれも読んでいないのだろうか？）

*1:大槻もこの式自体を「プライス方程式」と呼んでいて，やや違和感がある．これはプライス方程式を再帰的に代入して作られたマルチレベル淘汰基本方程式と呼ぶべきだろう